AFM
Category: Experimental Facilities
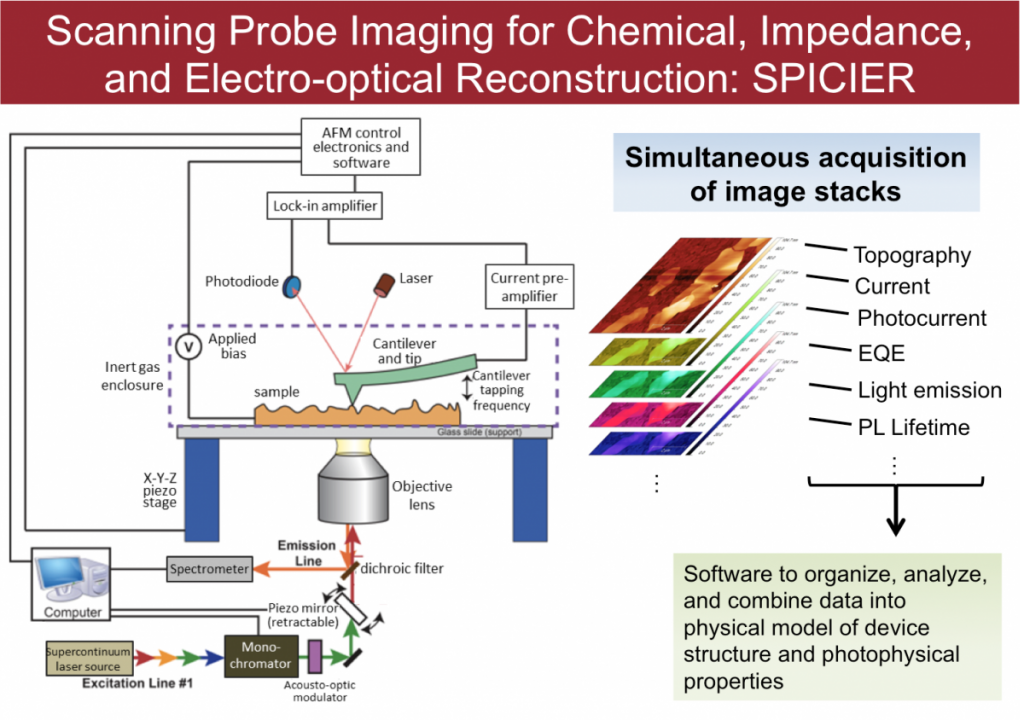
Figure. A schematic of the AFM setup: simultaneous image stacks for varying device parameters can be deconvoluted from a single-platform measurement, enabling correlation between material reactivity hotspots and nanoscale morphological features.
SPICIER is a state-of-the-art scanning probe instrument, which is a single experimental platform capable of simultaneous characterization of morphological, electronic, and optoelectronic properties of pre-assembled devices. The most significant advantage of the instrument is that it enables a correlation between topography and current (or photocurrent), and emission images at the nanometer-scale level without any complexity associated with lithographic and metal deposition process. Since all data points in each image are generated simultaneously with the identical experiment condition, accurate and reliable comparisons can be made with confidence.
References
1. Shih, C.-J.; Wang, Q. H.; Son, Y.; Jin, Z.; Blankschtein, D.; Strano, M. S., Tuning On-Off Current Ratio and Field Effect Mobility in a MoS2-Graphene Heterostructure via Schottky Barrier Modulation. ACS Nano 2014, 8, 5790-5798.
2. Son, Y.; Wang, Q. H.; Paulson, J. A.; Shih, C.-J.; Rajan, A. G.; Tvrdy, K.; Kim, S.; Alfeeli, B.; Braatz, R. D.; Strano, M. S., Layer Number Dependence of MoS2 Photoconductivity Using Photocurrent Spectral Atomic Force Microscopic Imaging. ACS Nano 2015, 9 , 2843-2855.
3. Son, Y.; Li, M.-Y.; Cheng, C.-C.; Wei, K.-H.; Liu, P.; Wang, Q. H.; Li, L.-J.; Strano, M. S., Observation of Switchable Photoresponse of a Monolayer WSe2–MoS2 Lateral Heterostructure via Photocurrent Spectral Atomic Force Microscopic Imaging. Nano Lett. 2016, 16 (6), 3571-3577.
NoRSE Algorithm
Abstract:
NoRSE was developed to analyze high-frequency data sets collected from multi-state, dynamic experiments, such as molecular adsorption and desorption onto carbon nanotubes. As technology improves sampling frequency, these stochastic data sets become increasingly large with faster dynamic events. More efficient algorithms are needed to accurately locate the unique states in each time trace. NoRSE adapts and optimizes a previously published noise reduction algorithm (Chung et al., 1991) and uses a custom peak flagging routine to rapidly identify unique event states. The algorithm is explained using experimental data from our lab and its fitting accuracy and efficiency are then shown with a generalized model of stochastic data sets. The algorithm is compared to another recently published state finding algorithm and is found to be 27 times faster and more accurate over 55% of the generalized experimental space. NoRSE is written as an M-file for Matlab.
Link to paper: http://bioinformatics.oxfordjournals.org/content/early/2011/11/14/bioinformatics.btr632
Supplied code: NoRSE Algorithm for MATLAB
function NoRSE
% Originally Coded by Nigel F. Reuel 4.01.2011
% Massachusetts Institue of Technology
% Department of Chemical Engineering
%
% Last Updated 10.27.2011
%
% NoRSE was developed to analyze high-frequency data sets collected
% from multi-state, dynamic experiments, such as molecular adsorption
% and desorption onto carbon nanotubes. Full description available in the
% Bioinformatics publication entitled, “NoRSE: Noise Reduction and State
% Evaluator for High-Frequency Single Event Traces” by NF Reuel et al.
%
% The code is written to be as general as possible, but there are a few
% parameters that can be modified by the user to improve fitting to their
% specific data sets. See lines quoted below for further discussion of
% these parameters.
%
% ^^^ User specified parameters in the noise reduction subroutine ^^^
%
% 1. p (line 163)
% 2. M (line 162)
% 3. N (line 160)
%
% ^^^ User specified parameters in the peak finder subroutine ^^^
%
% 1. nbins (line 65)
% 2. SW (line 262)
% 3. MoleL (line 297)
% 4. SigBinD (line 413)
%
% —– Step 1: Read in the Traces (can normalize here if desired) ——–
%
% Data Columns = Trace number , Data Rows = Time steps
%
RTD = csvread(‘Data.csv’);
%Determine the number of time steps (Ns) and number of transducers (Nt):
[Ns,Nt]= size(RTD);
RTD_n = RTD;
% Create empty matrix to recieve the noise reduced traces:
M = zeros(Ns,Nt);
%
% —————- Step 2: Denoise each of the Traces ——————–
%
%The denoising algorithm loses the first and last time steps, so set a new
%time window:
time = Ns – 2;
%Create an empty matrix to recieve the denoised trace data:
T_denoise = zeros(time,Nt);
for i = 1:Nt
NT = RTD_n(:,i);
IC = feval(@NoiseReduc,NT);
T_denoise(:,i) = IC(:,1);
end
% csvwrite([‘T_denoise’,int2str(iii),’.csv’],T_denoise);
%
%—————- Step 3: Construct APH for each trace ——————
%
% Number of bins for the histogram construction. We found 200 works well
% for experimental traces of ~1000 steps in length. You may need to
% decrease this for shorter traces or increase for longer.
%
% ^^^ NOTE: User can change following parameter to improve fit ^^^
%
nbins = 200;
%
%Create empty recieving matrices for histogram counts (nM) and the bin
%centers (xM)
nM = zeros(Nt,nbins);
xM = zeros(Nt,nbins);
for i = 1:Nt
Y = T_denoise(:,i);
[n,xout] = hist(Y,nbins);
nM(i,:) = n(1,:);
xM(i,:) = xout(1,:);
end
%xlswrite(‘nM’,nM);
%xlswrite(‘xM’,xM);
%
%—————- Step 4: Find peaks for each APH histrogram ————
%
%Use PeakFinder Function to find the Average Peak Locations (APL) – these
%translate to the bin number
APL = feval(@PeakFinder,nM,Ns);
[Nt,Nlev] = size(APL);
%
%Translate the APL bin numbers back to the normalized intensity level to
%determine the stochastic step levels (SLL)
SLL = zeros(Nt,Nlev);
for i = 1:Nt
% Very rarely, the peak finder will flag no bins as peaks, in this case
% we will use a general gaussian fit of the denoised data to find a
% mean step value.
if sum(APL(i,:)) == 0
Ncurves = 1;
X = T_denoise(i,:);
[u,~,~,~] = feval(@fit_mix_gaussian,X,Ncurves);
SLL(i,1) = u;
else
for j = 1:Nlev
if APL(i,j) ~= 0
N_bin = APL(i,j);
SLL(i,j) = xM(i,N_bin);
end
end
end
end
%
%———– Step 5 Determine the NoRSE Fit Trace —————
%
for ii = 1:Nt
RealT = T_denoise(:,ii);
count = 0;
for m = 1:Nlev
if SLL(ii,m) > 0
count = count + 1;
end
end
for i = 1:time
compare = zeros(count,1);
for j = 1:count
compare(j,1) = abs(RealT(i,1)-SLL(ii,j));
end
[C,I] = min(compare);
M(i+1,ii,1) = SLL(ii,I);
end
% Because the noise reduction program takes away the first and last time
% point, estimate their values as those immediately following and
% proceeding respectively
M(1,ii,1) = M(2,ii,1);
M(time+2,ii,1) = M(time+1,ii,1);
end
% Record the noise-reduced traces in a csv format:
csvwrite(‘NRData.csv’,M)
end
%
%
%
%
% <————–Functions embeded in the Trace Analyzer ————>
%
function IC = NoiseReduc(NT)
%
%Coded by Nigel Reuel on 8.31.2010
%
%Adaptation of Chung and Kennedy (1991) forward-backward non-linear
%filtering technique to reduce the noise of our
%fluorescent signal in an attempt to resolve the single molecule events
%amidst the noise.
%
%Input: Takes supplied noisy trace (NT)
%Output: Returns cleaned trace without the first and last data point
%
time = length(NT);
%
%Set algorithm parameters (discussion on this in Bioinformatics paper – Supplement A):
%
% ^^^ NOTE: User can change following parameter to improve fit ^^^
%
N = [4 8 16 32]; %Sampling window length
K = length(N); %Number of sampling windows
M = 10; %Weighting parameter length
P = 40; %Parameter that effects sharpness of steps
%
% ——– The Forward-Backward non-linear Algorithm ———–
%
%First – Run each time step and store the average forward and backward
%predictors for each of the sampling windows
%
I_avg_f = zeros(time,K);
I_avg_b = zeros(time,K);
for g = 1:time
%Run for each sampling window
for k = 1:K
%Solve for the average forward predictor (w/ some
%logic to help solve the beginning of the trace
window = N(k);
if g == 1
I_avg_f(g,k) = NT(1,1);
elseif g – window – 1 < 0
I_avg_f(g,k) = sum(NT(1:g-1,1))/g;
else
epoint = g – window;
spoint = g – 1;
I_avg_f(g,k) = sum(NT(epoint:spoint,1))/window;
end
%Now do the same for the backward predictor
if g == time
I_avg_b(g,k) = NT(g,1);
elseif g + window > time
sw = time – g;
I_avg_b(g,k) = sum(NT(g+1:time,1))/sw;
else
epoint = g + window;
spoint = g + 1;
I_avg_b(g,k) = sum(NT(spoint:epoint,1))/window;
end
end
end
%
%Second – Solve for non-normalized forward and backward weights:
f = zeros(time,K);
b = zeros(time,K);
for i = 1:time
for k = 1:K
Mstore_f = zeros(M,1);
Mstore_b = zeros(M,1);
for j = 0:M-1
t_f = i – j;
t_b = i + j;
if t_f < 1
Mstore_f(j+1,1) = (NT(i,1) – I_avg_f(i,k))^2;
else
Mstore_f(j+1,1) = (NT(t_f,1) – I_avg_f(t_f,k))^2;
end
if t_b > time
Mstore_b(j+1,1) = (NT(i,1) – I_avg_b(i,k))^2;
else
Mstore_b(j+1,1) = (NT(t_b,1) – I_avg_b(t_b,k))^2;
end
end
f(i,k) = sum(Mstore_f)^(-P);
b(i,k) = sum(Mstore_b)^(-P);
end
end
% Third – Solve for vector of normalization factors for the weights
C = zeros(time,1);
for i = 1:time
Kstore = zeros(K,1);
for k = 1:K
Kstore(k,1) = f(i,k) + b(i,k);
end
C(i,1) = 1/sum(Kstore);
end
% Fourth and final step – Put all parameters together to solve for the
% intensities
Iclean = zeros(time,1);
for i = 1:time
TempSum = zeros(K,1);
for k = 1:K
TempSum(k,1) = f(i,k)*C(i,1)*I_avg_f(i,k) + b(i,k)*C(i,1)*I_avg_b(i,k);
end
Iclean(i,1) = sum(TempSum);
end
IC = Iclean(2:time-1,1);
return
end
function PeakLocAvg = PeakFinder(nM,Ns)
% Coded by Nigel Reuel on 9.15.2010 updated in March 2011 by NFR
% This function finds the peaks of a histogram using a modified running
% average algorithm + peak flagging routine
%
[nT,nB] = size(nM);
%
% Size of window for running average algorithm (increasing this causes more
% of a rough approximation of peaks) User may need to vary for their
% specific data set)
%
% ^^^ NOTE: User can change following parameter to improve fit ^^^
%
SW = 3;
%
% Centered running average algorithm to help find peaks:
%
T_ra = zeros(nT,nB);
for j = 1:nT
for i = 1:nB
if i < (SW + 1)
T_ra(j,i) = sum(nM(j,1:i+SW))/(i+SW);
elseif i >= (SW+1) && i <= (nB-SW)
T_ra(j,i) = sum(nM(j,i-SW:i+SW))/(SW*2+1);
else
T_ra(j,i) = sum(nM(j,i:nB))/(nB-i+1);
end
end
end
%xlswrite(‘T_ra’,T_ra);
%
%———————-Peak finding algorithm—————————
%
% Base function on physical example of climbing up and down hills. Drop
% flags on supposed peaks. Eliminate “peaks” that are molehills. Combine
% peaks that are close neighbors.
Flags = zeros(nT,nB,6);
% Layer 1 = Peak Flag
% Layer 2 = Right Valley Bin#
% Layer 3 = Left Valley Bin#
% Layer 4 = Peak magnitude (Histogram Count)
% Layer 5 = Right Valley magnitude (Histogram Count)
% Layer 6 = Left Valley magnitude (Histogram Count)
% Molehill level (number of responses that are not significant – some fraction of the avg response)
%
%
% ^^^ NOTE: User can change following parameter to improve fit ^^^
%
MoleL = (Ns/nB/SW)*.5; % = #responses/#bins/SW ~= 1/2 of the Avg. Response – no significance.
% The multiplied factor (‘0.5’) can be decreased to allow smaller peak heights to be deemed ‘significant’
% or increased to allow for only the highest peaks to be flagged.
%
PeakLocAvg = zeros(nT,2);
for i = 1:nT
for j = 1:nB
if T_ra(i,j) > MoleL
% Logic to find significant peaks at endpoints (and the R/L
% valleys)
if j == 1 && T_ra(i,j) > T_ra(i,j+1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
Pval = T_ra(i,j);
Pnext = T_ra(i,j+1);
index = j;
% Find right hand valley:
while Pval > Pnext
index = index + 1;
Pval = T_ra(i,index);
Pnext = T_ra(i,index+1);
end
Flags(i,j,2) = index;
Flags(i,j,5) = T_ra(i,index);
elseif j == 1 && T_ra(i,j) <= T_ra(i,j+1)
Flags(i,j,1) = 0;
elseif j == nB && T_ra(i,j) > T_ra(i,j-1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
Pval = T_ra(i,j);
Pprior = T_ra(i,j-1);
index = j;
% Find left hand valley:
while Pval > Pprior
index = index – 1;
Pval = T_ra(i,index);
Pprior = T_ra(i,index-1);
end
Flags(i,j,3) = index;
Flags(i,j,6) = T_ra(i,index);
elseif j == nB && T_ra(i,j) <= T_ra(i,j-1)
Flags(i,j,1) = 0;
% Logic to find peaks at all midpoints (and their R/L valleys)
elseif T_ra(i,j) >= T_ra(i,j-1) && T_ra(i,j) >= T_ra(i,j+1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
% Find left hand valley:
Pval = T_ra(i,j);
Pprior = T_ra(i,j-1);
index = j;
if j > 2
Switch = 1;
else
Switch = 0;
index = 1;
end
while Pval > Pprior && Switch == 1;
index = index – 1;
Pval = T_ra(i,index);
Pprior = T_ra(i,index-1);
if index == 2
Switch = 0;
index = 1;
end
end
Flags(i,j,3) = index;
Flags(i,j,6) = T_ra(i,index);
% Find right hand valley:
Pval = T_ra(i,j);
Pnext = T_ra(i,j+1);
index = j;
if j < nB – 1
Switch = 1;
else
Switch = 0;
index = nB;
end
while Pval > Pnext && Switch == 1;
index = index + 1;
Pval = T_ra(i,index);
Pnext = T_ra(i,index+1);
if index == nB – 1;
Switch = 0;
index = nB;
end
end
Flags(i,j,2) = index;
Flags(i,j,5) = T_ra(i,index);
end
end
end
%{
X = (1:200)’;
Y1 = Flags(i,:,1)’;
Y2 = T_ra(i,:);
plot(X,Y1,X,Y2)
%}
%Make a vector containing the peak locations:
PeakVec = 0;
count = 1;
for j = 1:nB
if Flags(i,j,1) == 1
PeakVec(1,count) = j;
count = count + 1;
end
end
% Now analyze peak pairs:
% Specify significant peak valley distance and significant bin
% distance:
%
% ^^^ NOTE: User can change following parameter to improve fit. We found this parameter is analogous to that specified in line 297 ^^^
%
SigD = MoleL;
%
% ^^^ NOTE: User can change following parameter to improve fit ^^^
%
SigBinD = nB*(.025); % = 2.5% of the total bin #.
% Decreasing the multiplied factor (0.025) will allow for peaks closer
% together to remain unique, increasing the factor causes more of the
% flagged peaks to be unified into single ‘significant’ peaks.
%
%
Npeaks = length(PeakVec);
% Determine the peak pairwise interactions…each will have a right
% hand value and left hand value (except for the endpoints):
% 1: Unique
% 2: Combine
% 3: Ignore
% Create a matrix to recieve these calculations:
PeakCode = zeros(2,Npeaks); % Row1 = to right, Row2 = to left
for j = 1:Npeaks-1
% Determine the peak bin numbers:
PBN1 = PeakVec(1,j);
PBN2 = PeakVec(1,j+1);
% Calcualate the valley distances (left to right)
VD1 = abs(Flags(i,PBN1,4) – Flags(i,PBN1,5));
VD2 = abs(Flags(i,PBN2,6) – Flags(i,PBN2,4));
%
if VD1 <= SigD && VD2 <= SigD
% Combine
PeakCode(1,j) = 2;
PeakCode(2,j+1) = 2;
elseif VD1 >= SigD && VD2 <= SigD
% Left Peak sig, right peak ignore
PeakCode(1,j) = 1;
PeakCode(2,j+1) = 3;
elseif VD1 <= SigD && VD2 >= SigD
% Left peak ignore, right peak significant
PeakCode(1,j) = 3;
PeakCode(2,j+1) = 1;
elseif VD1 >= SigD && VD2 >= SigD
% Both peaks are significant
PeakCode(1,j) = 1;
PeakCode(2,j+1) = 1;
end
end
% Logic for the peak endpoints
Left = abs(Flags(i,PeakVec(1,1),4) – Flags(i,PeakVec(1,1),6));
if Left >= SigD
PeakCode(2,1) = 1;
else
PeakCode(2,1) = 3;
end
Right = abs(Flags(i,PeakVec(1,Npeaks),4) – Flags(i,PeakVec(1,Npeaks),5));
if Right >= SigD
PeakCode(1,Npeaks) = 1;
else
PeakCode(1,Npeaks) = 3;
end
% Now determine what to do with the peaks. Look at combinations
% reading left to right. Put signifcant peaks into a vector.
SPV = 0;
j = 1;
count = 1;
while j <= Npeaks
C1 = PeakCode(1,j);
C2 = PeakCode(2,j);
if C1 == 1 && C2 == 1
% This is a bonafide unique peak. Put it in the vector.
SPV(1,count) = PeakVec(1,j);
count = count + 1;
j = j+1;
elseif C1 == 2
% This peak will be merged with other peak(s)
count2 = 2;
Merge = PeakVec(1,j);
while C1 == 2
j = j + 1;
C1 = PeakCode(1,j);
Merge(1,count2) = PeakVec(1,j);
count2 = count2 + 1;
end
% Insert logic here to eliminate valleys and slow rises (see
% what is happening at the significant enpoints!)
End1 = Flags(i,Merge(1,1),4) – Flags(i,Merge(1,1),6);
End2 = Flags(i,Merge(1,end),4) – Flags(i,Merge(1,end),5);
Distance = Merge(1,end) – Merge(1,1);
if End1 >= SigD && End2 >= SigD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
elseif End1 >= SigD && End2 <= (SigD)*(-1) && Distance >= SigBinD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
elseif End1 <= SigD*(-1) && End2 >= (SigD) && Distance >= SigBinD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
end
else % Represents 1/3, 3/1, and 3/3 combos which are all ignored!!
j = j + 1;
end
end
Nsigpeaks = length(SPV);
for j = 1:Nsigpeaks
PeakLocAvg(i,j) = SPV(1,j);
end
%{
% Plot the PeakLocAvg to see how the algorithm performs)
S = Nsigpeaks;
FF = zeros(1,nB);
for k = 1:S
Temp = PeakLocAvg(i,k);
FF(1,Temp) = 1;
end
X = (1:200)’;
Y1 = FF(1,:)’;
Y2 = T_ra(i,:);
plot(X,Y1,X,Y2)
stop = 1;
%}
end
return
end
function [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% Gaussian Fit Function by Ohad Gal (c) 2003
% Download at:
% http://www.mathworks.com/matlabcentral/fileexchange/4222-a-collection-of-fitting-functions
% on 3.21.2011
%
% fit_mix_gaussian – fit parameters for a mixed-gaussian distribution using EM algorithm
%
% format: [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% input: X – input samples, Nx1 vector
% M – number of gaussians which are assumed to compose the distribution
%
% output: u – fitted mean for each gaussian
% sig – fitted standard deviation for each gaussian
% t – probability of each gaussian in the complete distribution
% iter- number of iterations done by the function
%
% initialize and initial guesses
N = length( X );
Z = ones(N,M) * 1/M; % indicators vector
P = zeros(N,M); % probabilities vector for each sample and each model
t = ones(1,M) * 1/M; % distribution of the gaussian models in the samples
u = linspace(min(X),max(X),M); % mean vector
sig2 = ones(1,M) * var(X) / sqrt(M); % variance vector
C = 1/sqrt(2*pi); % just a constant
Ic = ones(N,1); % – enable a row replication by the * operator
Ir = ones(1,M); % – enable a column replication by the * operator
Q = zeros(N,M); % user variable to determine when we have converged to a steady solution
thresh = 1e-3;
step = N;
last_step = inf;
iter = 0;
min_iter = 10;
% main convergence loop, assume gaussians are 1D
while ((( abs((step/last_step)-1) > thresh) & (step>(N*eps)) ) | (iter<min_iter) )
% E step
% ========
Q = Z;
P = C ./ (Ic*sqrt(sig2)) .* exp( -((X*Ir – Ic*u).^2)./(2*Ic*sig2) );
for m = 1:M
Z(:,m) = (P(:,m)*t(m))./(P*t(:));
end
% estimate convergence step size and update iteration number
prog_text = sprintf(repmat( ‘\b’,1,(iter>0)*12+ceil(log10(iter+1)) ));
iter = iter + 1;
last_step = step * (1 + eps) + eps;
step = sum(sum(abs(Q-Z)));
fprintf( ‘%s%d iterations\n’,prog_text,iter );
% M step
% ========
Zm = sum(Z); % sum each column
Zm(find(Zm==0)) = eps; % avoid devision by zero
u = (X’)*Z ./ Zm;
sig2 = sum(((X*Ir – Ic*u).^2).*Z) ./ Zm;
t = Zm/N;
end
sig = sqrt( sig2 );
return
end
NoRSE and SFA Comparison Code
- Category: NoRSE Code Files
function NoRSE_SFA_Comparison
% Finished by Nigel F. Reuel on 3.31.2011
% Massachusetts Institute of Technology
% Department of Chemical Engineering
%
% This code uses the generalized model of stochastic data sets to generate
% traces with embeded event states. It is currently set to compare NoRSE
% with the SFA algorithm. For each parameter set (A,B,C) it does the
% following:
%
% 1) Generates 100 traces
% 2) Fits traces with NoRSE
% 3) Fits traces with SFA
% 4) Computes average error for each algorithm
% 5) Reports the average times to run the 100 traces through NoRSE and SFA
%
% The errors and run times are then recorded in a *.csv file for further
% analysis.
%
% The program goes as follows:
%
% 1) Specify the trace generator parameters
%
A = 1;
B = [5 7 10 15 20 35 50 75 100 125 150 175 200 250 300 400 500];
C = [0.1 .15 .2 .3 .35 .4 .45 .5 .6 .7 .8 .85 .9 1 2 3 4 5 6 7 8 9 10];
% Number of traces:
nt = 100;
% Number of steps:
ns = 1000;
% Answer matrices:
NorseQual = zeros(length(B),length(C));
FSQual = zeros(length(B),length(C));
TimeN = zeros(length(B),length(C));
TimeFS = zeros(length(B),length(C));
%
for i = 1:length(B)
for j = 1:length(C)
b = B(i);
c = C(j);
disp([‘Analyzer started for condition B = ‘,num2str(b),’ and C = ‘,num2str(c)])
% 2) Generate Traces
M = feval(@GenTrace,A,b,c,nt,ns);
% 3) Generate Fits
[M2,T] = feval(@TraceFitter,M(:,:,2));
% 4) Compare Fits
% First you must specify the tolerance of fit:
TF = 0.02; %<— Remember this is on a scale of 0 to 1
% Reset the count of bad NoRSE points and bad FS points:
BadN = 0;
BadFS = 0;
for k = 1:nt
for l = 1:ns
if abs(M2(l,k,1)-M(l,k,1))> TF
BadN = BadN + 1;
end
if abs(M2(l,k,2)-M(l,k,1))> TF
BadFS = BadFS + 1;
end
end
end
% Now compute the percent error:
%disp(‘End of analysis. Run time and results below.’)
TotalSteps = nt*ns;
PerBN = BadN/TotalSteps;
PerBFS = BadFS/TotalSteps;
NorseQual(i,j) = PerBN;
FSQual(i,j) = PerBFS;
TimeN(i,j) = T(1,1);
TimeFS(i,j) = T(1,2);
end
end
% These are the output files:
csvwrite(‘BadFitPercentN.csv’,NorseQual)
csvwrite(‘BadFitPercentFS.csv’,FSQual)
csvwrite(‘TimeN.csv’,TimeN)
csvwrite(‘TimeFS.csv’,TimeFS)
return
end
function [M,T] = TraceFitter(RTD)
% This function fits the generated traces with both the NoRSE program and
% the fit states program.
% —– Step 1: Read in and the Traces ——–
%
%Determine the number of time steps (Ns) and number of transducers (Nt):
[Ns,Nt]= size(RTD);
RTD_n = RTD;
%
M = zeros(Ns,Nt,4); % First level Norse fit, second level FS
T = [0 0]; % 1 = NoRSE Time, 2 = FS time
%############# NoRSE ALGORITHM ############################################
%
% —————- Step 2: Denoise each of the Traces ——————–
%
tic
%The denoising algorithm loses the first and last time steps, so set a new
%time window:
time = Ns – 2;
%Create an empty matrix to recieve the denoised trace data:
T_denoise = zeros(time,Nt);
for i = 1:Nt
NT = RTD_n(:,i);
IC = feval(@NoiseReduc,NT);
T_denoise(:,i) = IC(:,1);
end
% csvwrite([‘T_denoise’,int2str(iii),’.csv’],T_denoise);
%
%—————- Step 3: Construct APH for each trace ——————
%
%Number of bins for the histogram construction?
nbins = 200;
%Create empty recieving matrices for histogram counts (nM) and the bin
%centers (xM)
nM = zeros(Nt,nbins);
xM = zeros(Nt,nbins);
for i = 1:Nt
Y = T_denoise(:,i);
[n,xout] = hist(Y,nbins);
nM(i,:) = n(1,:);
xM(i,:) = xout(1,:);
end
%xlswrite(‘nM’,nM);
%xlswrite(‘xM’,xM);
%
%—————- Step 4: Find peaks for each APH histrogram ————
%
%Use PeakFinder Function to find the Average Peak Locations (APL) – these
%translate to the bin number
APL = feval(@PeakFinder,nM);
[Nt,Nlev] = size(APL);
%
%Translate the APL bin numbers back to the normalized intensity level to
%determine the stochastic step levels (SLL)
SLL = zeros(Nt,Nlev);
for i = 1:Nt
% Very rarely, the peak finder will flag no bins as peaks, in this case
% we will use a general gaussian fit of the denoised data to find a
% mean step value.
if sum(APL(i,:)) == 0
Ncurves = 1;
X = T_denoise(i,:);
[u,~,~,~] = feval(@fit_mix_gaussian,X,Ncurves);
SLL(i,1) = u;
else
for j = 1:Nlev
if APL(i,j) ~= 0
N_bin = APL(i,j);
SLL(i,j) = xM(i,N_bin);
end
end
end
end
%
%———– Step 5 Determine the NoRSE Fit Trace —————
%
for ii = 1:Nt
RealT = T_denoise(:,ii);
count = 0;
for m = 1:Nlev
if SLL(ii,m) > 0
count = count + 1;
end
end
for i = 1:time
compare = zeros(count,1);
for j = 1:count
compare(j,1) = abs(RealT(i,1)-SLL(ii,j));
end
[C,I] = min(compare);
M(i+1,ii,1) = SLL(ii,I);
end
% Because the noise reduction program takes away the first and last time
% point, estimate their values as those immediately following and
% proceeding respectively
M(1,ii,1) = M(2,ii,1);
M(time+2,ii,1) = M(time+1,ii,1);
end
%
T(1,1) = toc;
%
%
% #############################################
%———- FitStates Analyzer —————- (Added 1.15.2011 by NFR)
% #############################################
%
%
tic
forward_trans = 0;
NonNormTraces = RTD;
[num_rows, num_cols] = size(NonNormTraces);
Ftime = 1:1:num_rows;
% Make empty matrix to recieve the traces and their fits
count = 0;
GoodTrace2 = 0;
for i = 1:num_cols
Tracemax = max(NonNormTraces(:,i));
Tracemin = min(NonNormTraces(:,i));
data3 = 1000*(NonNormTraces(:,i) – Tracemin)/(Tracemax – Tracemin);
data2 = 1000 – data3;
MaxNumofStates = 30;
maxN = 30;
[NumofStates, BestFitTraces] = fitStates(maxN, Ftime, data2, data3, MaxNumofStates);
M(:,i,2) = BestFitTraces; % Best fit trace from Fit States
end
T(1,2) = toc;
return
end
%
%
% <————–Functions embeded in the Trace Analyzer ————>
%
function IC = NoiseReduc(NT)
%
%Coded by Nigel Reuel on 8.31.2010
%
%Adaptation of Chung and Kennedy (1991) forward-backward non-linear
%filtering technique to reduce the noise of our
%fluorescent signal in an attempt to resolve the single molecule events
%amidst the noise.
%
%Input: Takes supplied noisy trace (NT)
%Output: Returns cleaned trace without the first and last data point
%
time = length(NT);
%
%Set algorithm parameters:
N = [4 8 16 32]; %Sampling window length
K = length(N); %Number of sampling windows
M = 10; %Weighting parameter length
P = 40; %Parameter that effects sharpness of steps
%
% ——– The Forward-Backward non-linear Algorithm ———–
%
%First – Run each time step and store the average forward and backward
%predictors for each of the sampling windows
%
I_avg_f = zeros(time,K);
I_avg_b = zeros(time,K);
for g = 1:time
%Run for each sampling window
for k = 1:K
%Solve for the average forward predictor (w/ some
%logic to help solve the beginning of the trace
window = N(k);
if g == 1
I_avg_f(g,k) = NT(1,1);
elseif g – window – 1 < 0
I_avg_f(g,k) = sum(NT(1:g-1,1))/g;
else
epoint = g – window;
spoint = g – 1;
I_avg_f(g,k) = sum(NT(epoint:spoint,1))/window;
end
%Now do the same for the backward predictor
if g == time
I_avg_b(g,k) = NT(g,1);
elseif g + window > time
sw = time – g;
I_avg_b(g,k) = sum(NT(g+1:time,1))/sw;
else
epoint = g + window;
spoint = g + 1;
I_avg_b(g,k) = sum(NT(spoint:epoint,1))/window;
end
end
end
%
%Second – Solve for non-normalized forward and backward weights:
f = zeros(time,K);
b = zeros(time,K);
for i = 1:time
for k = 1:K
Mstore_f = zeros(M,1);
Mstore_b = zeros(M,1);
for j = 0:M-1
t_f = i – j;
t_b = i + j;
if t_f < 1
Mstore_f(j+1,1) = (NT(i,1) – I_avg_f(i,k))^2;
else
Mstore_f(j+1,1) = (NT(t_f,1) – I_avg_f(t_f,k))^2;
end
if t_b > time
Mstore_b(j+1,1) = (NT(i,1) – I_avg_b(i,k))^2;
else
Mstore_b(j+1,1) = (NT(t_b,1) – I_avg_b(t_b,k))^2;
end
end
f(i,k) = sum(Mstore_f)^(-P);
b(i,k) = sum(Mstore_b)^(-P);
end
end
% Third – Solve for vector of normalization factors for the weights
C = zeros(time,1);
for i = 1:time
Kstore = zeros(K,1);
for k = 1:K
Kstore(k,1) = f(i,k) + b(i,k);
end
C(i,1) = 1/sum(Kstore);
end
% Fourth and final step – Put all parameters together to solve for the
% intensities
Iclean = zeros(time,1);
for i = 1:time
TempSum = zeros(K,1);
for k = 1:K
TempSum(k,1) = f(i,k)*C(i,1)*I_avg_f(i,k) + b(i,k)*C(i,1)*I_avg_b(i,k);
end
Iclean(i,1) = sum(TempSum);
end
IC = Iclean(2:time-1,1);
return
end
function PeakLocAvg = PeakFinder(nM)
% Coded by Nigel Reuel on 9.15.2010 updated in March 2011 by NFR
% This function finds the peaks of a histogram using a modified running
% average algorithm + peak flagging routine
%
[nT,nB] = size(nM);
%
%Size of window for running average algorithm (increasing this causes more
%of a rough approximation of peaks)
SW = 3;
% Centered running average algorithm to help find peaks:
%
T_ra = zeros(nT,nB);
for j = 1:nT
for i = 1:nB
if i < (SW + 1)
T_ra(j,i) = sum(nM(j,1:i+SW))/(i+SW);
elseif i >= (SW+1) && i <= (nB-SW)
T_ra(j,i) = sum(nM(j,i-SW:i+SW))/(SW*2+1);
else
T_ra(j,i) = sum(nM(j,i:nB))/(nB-i+1);
end
end
end
%xlswrite(‘T_ra’,T_ra);
%
%———————-Peak finding algorithm—————————
%
% Base function on physical example of climbing up and down hills. Drop
% flags on supposed peaks. Eliminate “peaks” that are molehills. Combine
% peaks that are close neighbors.
Flags = zeros(nT,nB,6);
% Layer 1 = Peak Flag
% Layer 2 = Right Valley Bin#
% Layer 3 = Left Valley Bin#
% Layer 4 = Peak magnitude (Histogram Count)
% Layer 5 = Right Valley magnitude (Histogram Count)
% Layer 6 = Left Valley magnitude (Histogram Count)
% Molehill level (number of responses that are not significant – avg!)
MoleL = (5/SW)*.5; % = #responses/#bins/SW = Avg. Response, no significance)
PeakLocAvg = zeros(nT,2);
for i = 1:nT
for j = 1:nB
if T_ra(i,j) > MoleL
% Logic to find significant peaks at endpoints (and the R/L
% valleys)
if j == 1 && T_ra(i,j) > T_ra(i,j+1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
Pval = T_ra(i,j);
Pnext = T_ra(i,j+1);
index = j;
% Find right hand valley:
while Pval > Pnext
index = index + 1;
Pval = T_ra(i,index);
Pnext = T_ra(i,index+1);
end
Flags(i,j,2) = index;
Flags(i,j,5) = T_ra(i,index);
elseif j == 1 && T_ra(i,j) <= T_ra(i,j+1)
Flags(i,j,1) = 0;
elseif j == nB && T_ra(i,j) > T_ra(i,j-1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
Pval = T_ra(i,j);
Pprior = T_ra(i,j-1);
index = j;
% Find left hand valley:
while Pval > Pprior
index = index – 1;
Pval = T_ra(i,index);
Pprior = T_ra(i,index-1);
end
Flags(i,j,3) = index;
Flags(i,j,6) = T_ra(i,index);
elseif j == nB && T_ra(i,j) <= T_ra(i,j-1)
Flags(i,j,1) = 0;
% Logic to find peaks at all midpoints (and their R/L valleys)
elseif T_ra(i,j) >= T_ra(i,j-1) && T_ra(i,j) >= T_ra(i,j+1)
Flags(i,j,1) = 1;
Flags(i,j,4) = T_ra(i,j);
% Find left hand valley:
Pval = T_ra(i,j);
Pprior = T_ra(i,j-1);
index = j;
if j > 2
Switch = 1;
else
Switch = 0;
index = 1;
end
while Pval > Pprior && Switch == 1;
index = index – 1;
Pval = T_ra(i,index);
Pprior = T_ra(i,index-1);
if index == 2
Switch = 0;
index = 1;
end
end
Flags(i,j,3) = index;
Flags(i,j,6) = T_ra(i,index);
% Find right hand valley:
Pval = T_ra(i,j);
Pnext = T_ra(i,j+1);
index = j;
if j < nB – 1
Switch = 1;
else
Switch = 0;
index = nB;
end
while Pval > Pnext && Switch == 1;
index = index + 1;
Pval = T_ra(i,index);
Pnext = T_ra(i,index+1);
if index == nB – 1;
Switch = 0;
index = nB;
end
end
Flags(i,j,2) = index;
Flags(i,j,5) = T_ra(i,index);
end
end
end
%{
X = (1:200)’;
Y1 = Flags(i,:,1)’;
Y2 = T_ra(i,:);
plot(X,Y1,X,Y2)
%}
%Make a vector containing the peak locations:
PeakVec = 0;
count = 1;
for j = 1:nB
if Flags(i,j,1) == 1
PeakVec(1,count) = j;
count = count + 1;
end
end
% Now analyze peak pairs:
% Specify significant peak valley distance and significant bin
% distance:
SigD = (5/SW)*.5; % = the average response
SigBinD = 200*(.025); % = 2.5% of the total bin #.
Npeaks = length(PeakVec);
% Determine the peak pairwise interactions…each will have a right
% hand value and left hand value (except for the endpoints):
% 1: Unique
% 2: Combine
% 3: Ignore
% Create a matrix to recieve these calculations:
PeakCode = zeros(2,Npeaks); % Row1 = to right, Row2 = to left
for j = 1:Npeaks-1
% Determine the peak bin numbers:
PBN1 = PeakVec(1,j);
PBN2 = PeakVec(1,j+1);
% Calcualate the valley distances (left to right)
VD1 = abs(Flags(i,PBN1,4) – Flags(i,PBN1,5));
VD2 = abs(Flags(i,PBN2,6) – Flags(i,PBN2,4));
%
if VD1 <= SigD && VD2 <= SigD
% Combine
PeakCode(1,j) = 2;
PeakCode(2,j+1) = 2;
elseif VD1 >= SigD && VD2 <= SigD
% Left Peak sig, right peak ignore
PeakCode(1,j) = 1;
PeakCode(2,j+1) = 3;
elseif VD1 <= SigD && VD2 >= SigD
% Left peak ignore, right peak significant
PeakCode(1,j) = 3;
PeakCode(2,j+1) = 1;
elseif VD1 >= SigD && VD2 >= SigD
% Both peaks are significant
PeakCode(1,j) = 1;
PeakCode(2,j+1) = 1;
end
end
% Logic for the peak endpoints
Left = abs(Flags(i,PeakVec(1,1),4) – Flags(i,PeakVec(1,1),6));
if Left >= SigD
PeakCode(2,1) = 1;
else
PeakCode(2,1) = 3;
end
Right = abs(Flags(i,PeakVec(1,Npeaks),4) – Flags(i,PeakVec(1,Npeaks),5));
if Right >= SigD
PeakCode(1,Npeaks) = 1;
else
PeakCode(1,Npeaks) = 3;
end
% Now determine what to do with the peaks. Look at combinations
% reading left to right. Put signifcant peaks into a vector.
SPV = 0;
j = 1;
count = 1;
while j <= Npeaks
C1 = PeakCode(1,j);
C2 = PeakCode(2,j);
if C1 == 1 && C2 == 1
% This is a bonafide unique peak. Put it in the vector.
SPV(1,count) = PeakVec(1,j);
count = count + 1;
j = j+1;
elseif C1 == 2
% This peak will be merged with other peak(s)
count2 = 2;
Merge = PeakVec(1,j);
while C1 == 2
j = j + 1;
C1 = PeakCode(1,j);
Merge(1,count2) = PeakVec(1,j);
count2 = count2 + 1;
end
% Insert logic here to eliminate valleys and slow rises (see
% what is happening at the significant enpoints!)
End1 = Flags(i,Merge(1,1),4) – Flags(i,Merge(1,1),6);
End2 = Flags(i,Merge(1,end),4) – Flags(i,Merge(1,end),5);
Distance = Merge(1,end) – Merge(1,1);
if End1 >= SigD && End2 >= SigD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
elseif End1 >= SigD && End2 <= (SigD)*(-1) && Distance >= SigBinD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
elseif End1 <= SigD*(-1) && End2 >= (SigD) && Distance >= SigBinD
SPV(1,count) = round(mean(Merge));
count = count + 1;
j = j + 1;
end
else % Represents 1/3, 3/1, and 3/3 combos which are all ignored!!
j = j + 1;
end
end
Nsigpeaks = length(SPV);
for j = 1:Nsigpeaks
PeakLocAvg(i,j) = SPV(1,j);
end
%{
% Plot the PeakLocAvg to see how the algorithm performs)
S = Nsigpeaks;
FF = zeros(1,nB);
for k = 1:S
Temp = PeakLocAvg(i,k);
FF(1,Temp) = 1;
end
X = (1:200)’;
Y1 = FF(1,:)’;
Y2 = T_ra(i,:);
plot(X,Y1,X,Y2)
stop = 1;
%}
end
return
end
%% ————————— FIT STATES ——————————–
function [NumofStates, BestFitTraces] = fitStates(maxN, time_vector, data2, data3, MaxNumofStates)
%This function determines the number of states for each trace
%INPUTS:
% maxN maximum number of transitions for each traces
% time_vector vector of times corresponding to each frame
% data2 second column of normalized data in *.dat files
% data3 third column of normalized data in *.dat files
%OUTPUTS
% NumofStates row vector containing number of states for each trace
% BestFitTraces matrix showing the current states occupied by each
% trace for each frame (crude approximation)
A{1} = time_vector’;
[row, cols] = size(data2); %# rows = # timeframes, # cols = # SWNT
for q = 1:1:cols %Loop through each SWNT trace
%redefine variable to match formatting used in StatesFinder
A{2} = data2(:,q);
A{3} = data3(:,q);
time=A{1};
data=A{3}./1000;
timeinc=time(2,1)-time(1,1);
fulldata=[A{1} A{2} A{3}];
fitdata=data;
antifit=data;
resultArray=zeros(maxN,3); %first column the begnning index. second column is the length. third colum is the step fit.
resultArray(1,1)=1;
resultArray(1,2)=length(data);
resultArray(1,3)=mean(data);
fitdata(:)=resultArray(1,3);
chisquaredFit=zeros(maxN,1);
chisquaredAntifit=zeros(maxN,1);
chisquaredFit(1)=sum((data-fitdata).^2,1);
SS=zeros(maxN,1);
SS(1)=1;
flag=0;
resultArray0 = resultArray;
for i=1:(maxN-1),
para=0;
for j=1:i,
temp=resultArray(j,1);
temp2=resultArray(j,2);
B=data(temp:(temp2+temp-1));
[StepSize,StepLocation,left,right]=TJstepFinder(B);
temp3=StepSize*(temp2)^0.5;
if temp3 > para %optimal num. of transitions (maximize temp3)
para=temp3;
newBegin1=temp;
newLength1=StepLocation-1;
newValue1=left;
newBegin2=temp+StepLocation-1;
newLength2=temp2-newLength1;
newValue2=right;
bestJ=j;
end
end
resultArray(bestJ,1)=newBegin1;
resultArray(bestJ,2)=newLength1;
resultArray(bestJ,3)=newValue1;
resultArray(i+1,1)=newBegin2;
resultArray(i+1,2)=newLength2;
resultArray(i+1,3)=newValue2;
currentFitArray=sort_on_key(resultArray(1:i+1,:),1);
antiFitArray=zeros(i+2,3);
antiFitArray(1,1)=1;
antiFitArray(1,2)=length(data);
for j=1:(i+1),
temp=currentFitArray(j,1);
temp2=currentFitArray(j,2);
if (temp2 == 1)
flag = 1;
break;
end
B=data(temp:(temp2+temp-1));
[StepSize,StepLocation,left,right]=TJstepFinder(B);
antiFitArray(j+1,1)=temp+StepLocation-1;
end
if (flag == 1)
break;
end
for j=1:i+1,
antiFitArray(j,2)=antiFitArray(j+1,1)-antiFitArray(j,1);
antiFitArray(j,3)=mean(data(antiFitArray(j,1):(antiFitArray(j,2)+antiFitArray(j,1)-1)));
end
antiFitArray(i+2,2)=length(data)-antiFitArray(i+2,1)+1;
antiFitArray(i+2,3)=mean(data(antiFitArray(i+2,1):end));
for j=1:i+1,
fitdata(resultArray(j,1):(resultArray(j,2)+resultArray(j,1)-1))=resultArray(j,3);
end
for j=1:i+2,
antifit(antiFitArray(j,1):antiFitArray(j,2)+antiFitArray(j,1)-1)=antiFitArray(j,3);
end
chisquaredFit(i+1)=sum((data-fitdata).^2,1);
chisquaredAntifit(i+1)=sum((data-antifit).^2,1);
SS(i+1)=chisquaredAntifit(i+1)/chisquaredFit(i+1);
resultArray0 = resultArray;
end
resultArray = resultArray0;
[C,I]=max(SS);
bestfitnumber=I;
resultArray(1,1)=1;
resultArray(1,2)=length(data);
resultArray(1,3)=mean(data);
fitdata(:)=resultArray(1,3);
chisquaredFit=zeros(maxN,1);
chisquaredFit(1)=sum((data-fitdata).^2,1);
for i=1:(bestfitnumber),
para=0;
for j=1:i,
temp=resultArray(j,1);
temp2=resultArray(j,2);
B=data(temp:(temp2+temp-1));
[StepSize,StepLocation,left,right]=TJstepFinder(B);
temp3=StepSize*(temp2)^0.5;
if temp3 > para,
para=temp3;
newBegin1=temp;
newLength1=StepLocation-1;
newValue1=left;
newBegin2=temp+StepLocation-1;
newLength2=temp2-newLength1;
newValue2=right;
bestJ=j;
end
end
resultArray(bestJ,1)=newBegin1;
resultArray(bestJ,2)=newLength1;
resultArray(bestJ,3)=newValue1;
resultArray(i+1,1)=newBegin2;
resultArray(i+1,2)=newLength2;
resultArray(i+1,3)=newValue2;
end
for j=1:bestfitnumber+1,
fitdata(resultArray(j,1):(resultArray(j,2)+resultArray(j,1)-1))=resultArray(j,3);
end
finalresult=sort_on_key(resultArray((1:bestfitnumber+1),:),1);
finalresult(:,1)=(finalresult(:,1)-1)*timeinc+time(1);
finalresult(:,2)=finalresult(:,2)*timeinc;
if MaxNumofStates == 10 %if maximum number of states is 10
statesnum=length(unique(round(10*finalresult(:,3))));
rounded_fit = round(fitdata*10)/10;
fitdata_average = zeros(1,length(fitdata));
for i = 1:1:length(rounded_fit)
if rounded_fit(i) ~= -1
sameState_coord = find(rounded_fit==rounded_fit(i));
total_sum = 0;
for j = 1:1:length(sameState_coord)
total_sum = total_sum+fitdata(sameState_coord(j));
rounded_fit(sameState_coord(j)) = -1;
end
average_state = total_sum/(length(sameState_coord));
for k = 1:1:length(sameState_coord)
fitdata_average(sameState_coord(k)) = average_state;
end
end
end
else %if maximum number of states is something other than 10
%from the fit, group states with similar values according to the
%maximum numnber of states as specified by the user. First, create a
%vector of states between 0 and 1 consisting of number of states
%specified by the user. Then find the difference between each of these
%states and the fitdata value, and whichever state i closest to the
%fitdata value is determined to be the state.
possible_states = 0:(1/MaxNumofStates):1;
rounded_fit = zeros(1, length(fitdata));
for i = 1:1:length(fitdata)
difference = abs(fitdata(i)-possible_states);
[dum, state_coord] = min(difference); %find the state closest to the fit data
rounded_fit(i) = possible_states(state_coord);
end
%Now start to average all the states that were grouped into having the
%same rounded state
fitdata_average = zeros(1,length(fitdata));
for i = 1:1:length(rounded_fit)
if rounded_fit(i) ~= -1
sameState_coord = find(rounded_fit==rounded_fit(i));
total_sum = 0;
for j = 1:1:length(sameState_coord)
total_sum = total_sum+fitdata(sameState_coord(j));
rounded_fit(sameState_coord(j)) = -1;
end
average_state = total_sum/(length(sameState_coord));
for k = 1:1:length(sameState_coord)
fitdata_average(sameState_coord(k)) = average_state;
end
end
end
statesnum = length(unique(fitdata_average));
end
output(q,:) = [statesnum, fitdata_average];
end
NumofStates = output(:,1)’;
BestFitTraces = output(:, 2:end)’;
return;
end
%% ———————– TJ STEP FINDER ———————————
function [StepSize,StepLocation,left,right]=TJstepFinder(B)
%This function is called upon by the fitStates function to locate steps in
%the traces.
global C; %this is what we send to TJflatFit
lengthB=length(B);
%Initial conditions
fitResult=B;
tempfit=B;
StepSize=0;
bestchisquared=10^10;
time=(1:lengthB);
StepLocation=1;
C=zeros(1,2);
C(:,1)=(1:1)’;
C(:,2)=B(1:1);
A1=mean(C(:,2));
tempfit(1:1)=A1;
C=zeros((lengthB-1),2);
C(:,1)=((1+1):lengthB)’;
C(:,2)=B((1+1):lengthB);
A2=mean(C(:,2));
StepSize=abs(A2-A1);
left=A1;
right=A2;
for i=1:(lengthB-1),
C=zeros(i,2);
C(:,1)=(1:i)’;
C(:,2)=B(1:i);
A1=mean(C(:,2));%fmins(‘TJflatFit’,mean(C(:,2)));
tempfit(1:i)=A1;
C=zeros((lengthB-i),2);
C(:,1)=((i+1):lengthB)’;
C(:,2)=B((i+1):lengthB);
A2=mean(C(:,2));%fmins(‘TJflatFit’,mean(C(:,2)));
tempfit((i+1):lengthB)=A2;
chisquared=sum((tempfit-B).^2,1);
if chisquared < bestchisquared,
bestchisquared=chisquared;
fitResult=tempfit;
StepSize=abs(A2-A1);
StepLocation=i+1;
left=A1;
right=A2;
end
end
return;
end
%% ———————–SORT ON KEY ————————————-
function sorteer=sort_on_key(rij,key)
%This function is called upon by the fitStates function to locate steps in
%the traces. It reads a (index,props) array ands sorts along the index with one of the
%props as sort key
size=length(rij(:,1));
sorteer=0*rij;
buf=rij;
for i=1:size
[g,h]=min(buf(:,key));
sorteer(i,:)=buf(h,:);
buf(h,key)=max(buf(:,key))+1;
end
return;
end
function M = GenTrace(A,B,C,numTr,Ttotal)
% Coded by Nigel Reuel on 3.3.2011
% This function generates general step traces according to three
% parameters which encompass all types of step data:
% A – tendency up / tendency down
% B – avg event time / signal sampling time
% C – avg step size / avg noise
% It generates a user-specified number of traces with these three
% parameters and returns a 3D matrix of the traces (first level – real
% response, 2nd level – noise). To aid in comparing traces, all traces are
% normalized on a scale of 0 to 1.
%
%
Tdown = 1;
Tup = A;
Tprob = Tdown + Tup;
%SigSampT = 1; %< — Not used, but coded in my index numbers
AvgEventT = B;
AvgNoise = 1;
AvgStep = C;
%
% Set total simulation time and number of traces: – Now function input
% Ttotal = 1000;
% Initialize solution matrix:
M = zeros(Ttotal,numTr,2);
% Generate the traces
for i = 1:numTr
t = 1;
% Signal start (arbitrary due to normalization):
S = 100;
% Track signal changes:
SigChange = [0 0];
num = 1;
while t < Ttotal
SigChange(num,1) = t;
% 1) Determine step size:
SS = rand()*2*AvgStep;
% 2) Determine the direction:
rand1 = rand();
check1 = rand1*Tprob;
if check1 < Tdown
S = S – SS;
else
S = S + SS;
end
SigChange(num,2) = S;
num = num + 1;
% 3) Determine the next event time:
tstep = rand()*2*AvgEventT;
t = t + tstep;
end
% Turn signal change matrix into real trace and trace w/ noise
Real_Tr = zeros(Ttotal,1);
Noise_Tr = zeros(Ttotal,1);
Intervals = round(SigChange(:,1));
Intervals(num,1) = Ttotal;
for j = 1:num-1
for k = Intervals(j,1):Intervals(j+1,1)
Real_Tr(k,1) = SigChange(j,2);
NoiseL = (rand()*2-1)*AvgNoise;
Noise_Tr(k,1) = SigChange(j,2) + NoiseL;
end
end
%Normalize according to max and min levels in traces
Max(1,1) = max(Real_Tr);
Max(2,1) = max(Noise_Tr);
Min(1,1) = min(Real_Tr);
Min(2,1) = min(Noise_Tr);
MaxN = max(Max);
MinN = min(Min);
SigDiff = MaxN-MinN;
Real_n = (Real_Tr-MinN)./SigDiff;
Noise_n = (Noise_Tr-MinN)./SigDiff;
M(:,i,1) = Real_n;
M(:,i,2) = Noise_n;
% Graphical check of traces:
%{
X = 1:1000;
X = X’;
plot(X,Real_n,X,Noise_n);
%}
end
return
end
function [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% Gaussian Fit Function by Ohad Gal (c) 2003
% Download at:
% http://www.mathworks.com/matlabcentral/fileexchange/4222-a-collection-of-fitting-functions
% on 3.21.2011
%
% fit_mix_gaussian – fit parameters for a mixed-gaussian distribution using EM algorithm
%
% format: [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% input: X – input samples, Nx1 vector
% M – number of gaussians which are assumed to compose the distribution
%
% output: u – fitted mean for each gaussian
% sig – fitted standard deviation for each gaussian
% t – probability of each gaussian in the complete distribution
% iter- number of iterations done by the function
%
% initialize and initial guesses
N = length( X );
Z = ones(N,M) * 1/M; % indicators vector
P = zeros(N,M); % probabilities vector for each sample and each model
t = ones(1,M) * 1/M; % distribution of the gaussian models in the samples
u = linspace(min(X),max(X),M); % mean vector
sig2 = ones(1,M) * var(X) / sqrt(M); % variance vector
C = 1/sqrt(2*pi); % just a constant
Ic = ones(N,1); % – enable a row replication by the * operator
Ir = ones(1,M); % – enable a column replication by the * operator
Q = zeros(N,M); % user variable to determine when we have converged to a steady solution
thresh = 1e-3;
step = N;
last_step = inf;
iter = 0;
min_iter = 10;
% main convergence loop, assume gaussians are 1D
while ((( abs((step/last_step)-1) > thresh) & (step>(N*eps)) ) | (iter<min_iter) )
% E step
% ========
Q = Z;
P = C ./ (Ic*sqrt(sig2)) .* exp( -((X*Ir – Ic*u).^2)./(2*Ic*sig2) );
for m = 1:M
Z(:,m) = (P(:,m)*t(m))./(P*t(:));
end
% estimate convergence step size and update iteration number
prog_text = sprintf(repmat( ‘\b’,1,(iter>0)*12+ceil(log10(iter+1)) ));
iter = iter + 1;
last_step = step * (1 + eps) + eps;
step = sum(sum(abs(Q-Z)));
fprintf( ‘%s%d iterations\n’,prog_text,iter );
% M step
% ========
Zm = sum(Z); % sum each column
Zm(find(Zm==0)) = eps; % avoid devision by zero
u = (X’)*Z ./ Zm;
sig2 = sum(((X*Ir – Ic*u).^2).*Z) ./ Zm;
t = Zm/N;
end
sig = sqrt( sig2 );
return
end